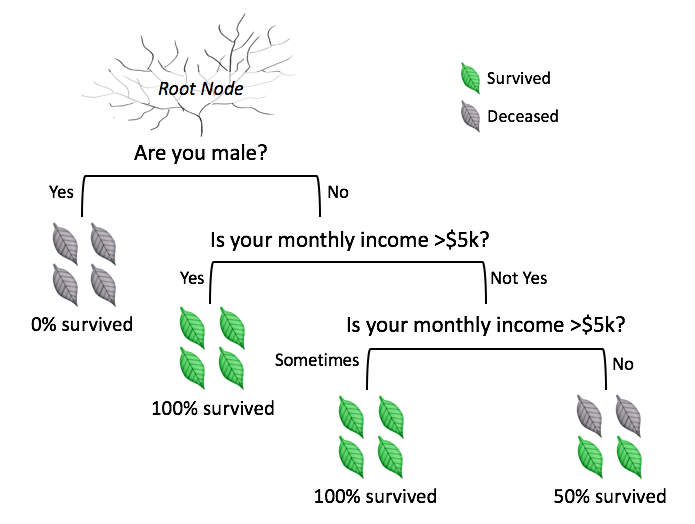
1. Giải thuật ID3:
ID3_algorithm(Training_Set, Class_Labels, Attributes)
Tạo nút Root của cây quyết định
If tất cả các ví dụ của Training_Set thuộc cùng lớp c
Return Cây quyết định có nút Root được gắn với (có nhãn) lớp c
If Tập thuộc tính Attributes là rỗng
Return Cây quyết định có nút Root được gắn với nhãn lớp ≡ Majority_Class_Label(TrainingSet)
A ← Thuộc tính trong tập Attributes có khả năng phân loại “tốt nhất” đối với Training_Set
Thuộc tính kiểm tra cho nút Root ← A
For each Giá trị có thể v của thuộc tính A
Bổ sung một nhánh cây mới dưới nút Root, tương ứng với trường hợp: “Giá trị của A là v”
Xác định Training_Setv = {ví dụ x | x ⊆ Training_Set, xA=v}
If (Training_Setv là rỗng) Then
Tạo một nút lá với nhãn lớp ≡ Majority_Class_Label(Training_Set)
Gắn nút lá này vào nhánh cây mới vừa tạo
Else Gắn vào nhánh cây mới vừa tạo một cây con sinh ra bởi ID3_algorithm(Training_Setv, Class_Labels, {Attributes A})
Return Root
2. Giao diện chính của chương trình Demo gồm 4 phần:
o Phần 1: Bảng lưu dữ liệu training (Data Training).
o Phần 2: Ghi ra các bước giải của thuật toán (Solutions).
o Phần 3: Vẽ cây minh họa cho thuật toán (Decision Tree).
o Phần 4: Các chức năng của chương trình (Control).
Có 4 button với các chức năng như sau:
- Load Data: Đưa dữ liệu training vào chương trình.
- ID3 – Alg: Chạy giải thuật ID3.
- Reset: Khởi động, chạy lại chương trình.
- About: Thông tin về chương trình.
3. Các bước chạy chương trình:
- Đầu tiên, nạp dữ liệu vào chương trình bằng button Load Data.
Dữ liệu được đưa lên bảng Data Training (Phần 1).
- Sau đó, nhấn button ID3 – Alg để chạy giải thuật.
Các bước giải sẽ được hiện ra ở phần 2 (Solutions).
Cây được vẽ ra ở phần 3 (Decision Tree).
4. Giao diện chương trình:

Chương trình gồm những hàm chính sau:
Hàm tính Entropy:
· Công thức: Entropy (S) = – p+ log2 p+ – p- log2 p-
· Code [C#]:
private double GetEntropy(int Positives , int Negatives)
{
if (Positives == 0)
return 0;
if (Negatives == 0)
return 0;
double Entropy;
int total = Negatives + Positives;
double RatePositves = (double)Positives / total;
double RateNegatives = (double)Negatives / total;
Entropy = -RatePositves * Math.Log(RatePositves, 2) – RateNegatives * Math.Log(RateNegatives, 2);
return Entropy;
}
Hàm tính Gain:
· Công thức:

· Code [C#]:
private double Gain(List<List<string>> Examples, Attribute A, string bestat)
{
double result;
int CountPositives = 0;
int[] CountPositivesA = new int[A.Value.Count];
int[] CountNegativeA = new int[A.Value.Count];
int Col = Attributes.IndexOf(A);
for (int i = 0; i < A.Value.Count; i++)
{
CountPositivesA[i] = 0;
CountNegativeA[i] = 0;
}
for (int i = 0; i < Examples.Count; i++)
{
int j = A.Value.IndexOf(Examples[i][Col].ToString());
if (Examples[i][Examples[0].Count – 1]==”yes”)
{
CountPositives++;
CountPositivesA[j]++;
}
else
{
CountNegativeA[j]++;
}
}
result = GetEntropy(CountPositives, Examples.Count – CountPositives);
for (int i = 0; i < A.Value.Count; i++)
{
double RateValue = (double)(CountPositivesA[i] + CountNegativeA[i]) / Examples.Count;
result = result – RateValue * GetEntropy(CountPositivesA[i], CountNegativeA[i]);
}
Solution = Solution + “n * Gain(” + bestat + “,” + A.Name + “) = ” + result.ToString();
return result;
}
Hàm chọn đặc tính tốt nhất:
· Phương pháp:
- Dựa vào giá trị gain của các đặc tính, đặc tính nào có Gain lớn nhất.
- Chọn đặc tính đó – đặc tính tốt nhất.
· Code [C#]:
private Attribute GetBestAttribute(List<List<string>> Examples, List<Attribute> Attributes, string bestat)
{
double MaxGain = Gain(Examples, Attributes[0], bestat);
int Max = 0;
for (int i = 1; i < Attributes.Count; i++)
{
double GainCurrent = Gain(Examples, Attributes[i], bestat);
if (MaxGain < GainCurrent)
{
MaxGain = GainCurrent;
Max = i;
}
}
return Attributes[Max];
}
Hàm thực hiện giải thuật ID3:
Code:
private TreeNode ID3(List<List<string>> Examples, List<Attribute> Attribute,string bestat)
{
if (CheckAllPositive(Examples))
{
return new TreeNode(new Attribute(“Yes”));
}
if (CheckAllNegative(Examples))
{
return new TreeNode(new Attribute(“No”));
}
if (Attribute.Count == 0)
{
return new TreeNode(new Attribute(GetMostCommonValue(Examples)));
}
Attribute BestAttribute = GetBestAttribute(Examples, Attribute, bestat);
int LocationBA = Attributes.IndexOf(BestAttribute);
TreeNode Root = new TreeNode(BestAttribute);
for (int i = 0; i < BestAttribute.Value.Count; i++)
{
List<List<string>> Examplesvi = new List<List<string>>();
for (int j = 0; j < Examples.Count; j++)
{
if (Examples[j][LocationBA].ToString() == BestAttribute.Value[i].ToString())
Examplesvi.Add(Examples[j]);
}
if (Examplesvi.Count==0)
{
return new TreeNode(new Attribute(GetMostCommonValue(Examplesvi)));
}
else
{
Attribute.Remove(BestAttribute);
Root.AddNode(ID3(Examplesvi, Attribute,BestAttribute.Value[i]));
}
}
return Root;
}